Data is a somewhat amorphous thing; it can be lots of things depending on who
uses the word and what he intends it to describe. The data of mythology would
include unicorns while the data of biology would not. Data exists in each case but
of entirely different kinds. Data in terms of a computer is not necessarily
the same as data when discussing a computer network. There is data that is
processed by a machine and is not really intended to be meaningful to the
machine operator. Fortunately we're only concerned here with machines and
they always use data in a numerical form, namely binary digits.
A binary digit is called a bit and has only one of two values:
it is either a zero or a one. There are no gradations, no gray areas, no
ambiguity. A bit it always either a zero or a one so data is this sense is
pretty one dimensional. These bits accumulate into strings of varying lengths.
Each of these accumulations has a fixed minimum and maximum value. The one
accumulation often encountered is called a byte and is a collection of
eight bits. These bits number from zero to seven counting from the right. This
makes the bit on the right (bit zero) the "least significant bit" and the one
on the left the "most significant bit".
Computer data is processed in bytes. The individual bits are important based on their position within the byte. These bytes can be combined into still larger
data units usually determined by the size of the CPU "registers".
Some CPUs can process four bytes (32 bits) as one piece, others go up to 64 bits A CPU
(microprocessor) understands data as either instructions or
data and based on
the kind of input it's working with, the bits have different meanings. A CPU
instruction is determined by which bits in the instruction are "set"
(equal to one, usually). The
data is what the instruction works on (processes). The CPU doesn't always look at
the individual bits in the data, only in the instructions it receives. There are cases
where the position of a bit in a larger string of bits it significant.
We're still using bits and bytes but they are used differently at this level.
The easiest way to visualize this is to look at something we commonly use
such as an IP address used to navigate around the Internet:
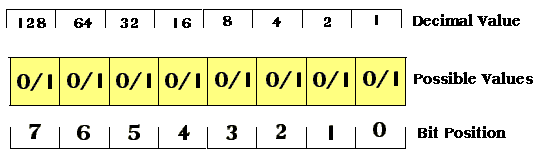
A byte has eight bits. Each of these bits is used to represent a decimal value.
Beginning at the right, bit 0 (zero) has the decimal value of 1 if the bit
is set to one.
Bit 2 will have a value of 2 if set to one. If the bits are
added together the sum will be a decimal number, 3.
Notice that the IP address 192.168.2.100 is divided into four bytes
and that each has a decimal value derived from adding together the bits set
to one (1) within that byte.
To get 192 we add together the bits starting
at the left end of the address up to the first dot (the 8 bits between each dot is
called an octet). Bit 7 in the leftmost octet has a value of 128 if it is set to a one. That's less
than 192 so we try the next bit. This bit has a value of 64 so we add it to
128 add we get 192. Since this matches the number we're looking for, all
the other bits are left as zeroes and we move to the next "octet" and do
the same calculation for it.
We do this for all the bytes. Obviously you can determine the actual bit
oriented address by doing the same thing in reverse. All of this is to
demonstrate that bits and bytes can be used in various ways to represent
various things. This example is most likely to be understandable to
those not familiar with the way machines "think". There's other examples of
how something as simple as a binary number can do really complicated things
but the intelligence of these operations resides with the people who make
it all work.
An Internet IP address uses this scheme to convert a 32 bit binary number
into the familiar "Dotted-Quad", four decimal numbers separated by a "dot"
(the period character). A DNS (IP to name) server will further convert this
decimal number into a "name" like, www.acme.net (and of course convert it back again
if needed).

|
There are several numbering systems used in digital electronics. The only
one that an electronic device uses is binary since all it can recognize is
either the presence or absence of an electrical current through its
circuits. This is, obviously, just one of two possible states. The human
operator uses other numbering systems for his or her convenience. These
other systems are chosen based on how many bits the person wants to
manipulate and the kind of circuit involved.
Since the original digital
circuits were limited to four or eight bits per operation, the Octal
numbering system (base 8) is apparent everywhere. The ASCII codes and ANSI
Escape Sequences, modem commands, serial and parallel ports, Keyboard Scan
Codes and lots of other encoding schemes all use octal numbering. This is
also the basic data unit, the byte (8 bits).
Hexadecimal (base 16) is another convenient number system since it
allows one to represent any of 16 bits with just one digit. Decimal (base
10) is used only to make numbers easier for humans to comprehend and are
not used within a digital system at all. These different numbering systems
are usually only important to programmers since the electronics can only be
accessed with binary values.
|
|
|
Decimal | Hex | Octal | Binary
|
|
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
|
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
|
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
|
|

